Difference between Actual, Standard and Normal Flows

What are Normal Conditions of Temperature and Pressure?

1. Difference between Actual, Standard and Normal Flows

1.1. What are Normal Conditions of Temperature and Pressure?

This article brings you detailed information regarding normal conditions of temperature and pressure and try to solve questions like:

How to convert actual flow to normal flow?
How to convert standard cubic meter to normal cubic meter?
How actual to normal flow conversion works?

If you need to do any calculation regarding this topic feel free to use our Flow Rate Calculator

Actual, Standard or Normal Flows

2. Overview

Gas density changes with pressure and temperature, so the use of standardized volumes when referring to quantities of gas is mandatory.

Standardized volumes are commonly used in different types of industries which uses gas as raw material. The volume of gas at actual pressure and temperature must be converted to standardized volumes.

The two common standardized volumes are standard cubic feet (scf) and normal cubic meters (Nm3).

A standard cubic foot of gas corresponds to 1 cubic foot of gas at 32 °F (0 °C) and 14.6959 PSI, and a normal cubic meter of gas corresponds to 1 cubic meter at 20°C at 101.325 kPa (NIST Reference). We will see later that it is important to list the temperature and pressure being used as standard, since many standards are used worldwide.

2.1. Why we use the standardized flows instead of simple volumetric flow?

We use standardized flows to make calculations easy.

For example, if we are compressing 125 Nm3/min air from 1 bar to 25 bar pressure then the volumetric flow through the compressor will remains same in Nm3/min but this is not the case for the volumetric flow in actual conditions.

The gas being compressible, it is possible to change a volume of the same amount of gas by compressing or changing its temperature.

It becomes very difficult to define a quantity of gas volume without relating this value with the pressure and temperature when the volume was measured.

Usually is not easy to define the temperature and pressure of a volume of gas, this is why normally we use standardized volumes referred to a define set of temperature and pressure measurements. We call this conditions normalized or standard.

2.2. STP vs NTP

STP means Standard Temperature and Pressure.
NTP means Normal Temperature and Pressure.

2.3. Normal Cubic Meter (nm3/h) vs Actual Cubic Meter (am3/h)

Nm3/h refers to flow of gas at normal temperature and pressures.
Am3/h refers to flow of gas at current operating conditions of the process.

3. What are the standard temperature and pressure applications?

Standard or normal conditions are used as reference values in thermodynamics of gases. To specify the gas volume, Normal or Standard temperature and pressure conditions are generally used.

The reason is very simple, the volume of a constant number of moles of gas depends on the measurements of temperature and pressure.

Due to this reason, whenever the quantity of gas is specified in terms of gas volume, it is necessary to define the corresponding temperature and pressure conditions for the volume measurement.

Therefore, we can use the reference temperature and pressure conditions to specify the volume of gas measured under those conditions. Once the volume is calculated, we can convert the calculated amount into an amount of moles or mass of gas.

There are different standards that define different temperature and pressure values. These standards depend on the organization that defines them. In general, the standard pressure is close to atmospheric pressure and the standard temperature is close to the ambient temperature value.

4. Gas properties

The gases by definition are in a gaseous state, under defined pressure and temperature (for example, the nitrogen we breathe). Steam and vapors are liquids in the conditions described above, although thermodynamically there is no difference between vapor / vapors and gases.

A fundamental difference between liquids and gases is their compressibility (liquids are generally considered incompressible). The compressibility is a property of the matter to which it causes that all the bodies diminish of volume when subjecting them to a pressure or compression determined keeping other parameters constant.

Another important property of gases is that their volume will increase with the increase in temperature, a property of the gas used in hot air balloons.

STP and NTP Flow

The description of the relationship of these properties is given by the Law of Ideal Gas:

PVnRT

where (in SI metric units):

P = the gas absolute pressure, in Pa
n = number of moles, in mol
V = the gas molar volume, in m3/mol
T = the gas absolute temperature, in K
R = the universal gas law constant of 8.314472 m3·Pa·mol-1·K-1

or where (in customary USA units):

P = the gas absolute pressure, in psia
n = number of moles, in lb-mol
V = the gas molar volume, in ft3/lb-mol
T = the gas absolute temperature, in degrees Rankine (°R)
R = the universal gas law constant of 10.7316 ft3·psia·lb-mol-l·°R-1

The mass of a gas will remain constant but the volume and density will change with pressure and temperature (law of conservation of mass).

If you need to do any calculation regarding this topic feel free to use our Flow Rate Calculator:

flow-rate-calculator.html 'Flow Rate Calculator'

For this reason, we will use mass instead of volume as a much more relevant term for measuring.

Usually, gases like compressed air or natural gas are measured using standardized molar volume (eg Scf or Nm3).

These terms at the first glance look like volumetric terms, which they are not. Corrected Volume is defined as mass over the density at reference conditions (eg at 0°C and 1013.25mbar; 1.29kg/m3 for air), thus it is a mass term.

A volumetric flow rate with units of CFM or m3 implies that the flow rate was measured at actual conditions (actual pressure, actual temperature).

The distinction between Standardized and Actual is important because it implies that his density changes with pressure and temperature.

This can be seen from taking a look at the ideal gas law. As you may remember, density = mass/volume.

When the ideal gas law is rearranged, the gas density can be seen to be proportional to pressure, and inversely proportional to temperature.

Density Formula based on Ideal Gas Law

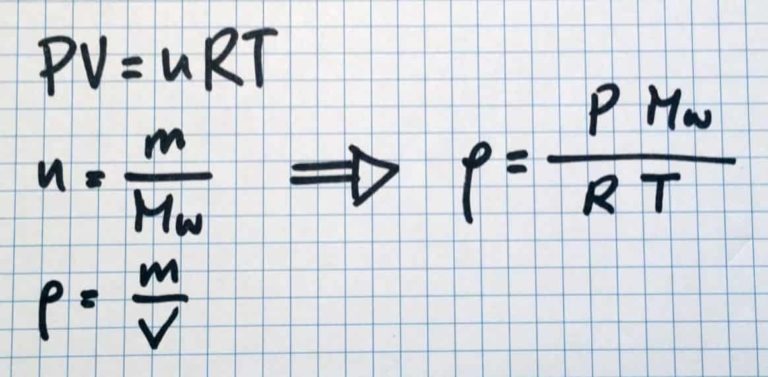
If we take Air for example, Air density at standard conditions is .0752 lb/ft3.

Since the air density of an air flow stated at standard conditions (SCFM) is always the same, it is essentially a mass flow rate!

Stating an air flow in units of SCFM makes it easy to compare conditions, and certain calculations simpler.

ρ = m/V → m = ρV →m/t = ρ (V/t)

mass flow rate = density* Volumetric flow rate.

In systems with vacuum pumps, blowers, compressors, and heat exchangers, air pressure and temperature are constantly changing, which means the actual volume flow is changing. This makes the specification of volume flow particularly prone to error and misinterpretation. Unless there is a leak, the mass / standard volume flow stays the same, so it is more concise to discuss these systems in terms of mass or standard volume flow. Specify mass or standard volume ...be understood!

Usually, Normal Volume is considered as a unit of mass for gases equal to the mass of the reference volume measured at a pressure and temperature of reference conditions.

For example, Ndm3 is a unit of mass for gases equal to the mass of 1 liter (0.035 3147 ft3) at a pressure of 1 atmosphere and at a standard temperature, often 0 °C (32 °F) or 20 °C (68 °F).

To convert from Normal or Standard Conditions to Actual (Operating) Conditions the molar gas volume is needed.

The molar gas volumes can be calculated with an accuracy that is usually sufficient by using the ideal gas law:

PV=nRT

where (in SI metric units):

P = the gas absolute pressure, in Pa
n = number of moles, in mol
V = the gas molar volume, in m3/mol
T = the gas absolute temperature, in K
R = the universal gas law constant of 8.314472 m3·Pa·mol-1·K-1

or where (in customary USA units):

P = the gas absolute pressure, in psia
n = number of moles, in lb-mol
V = the gas molar volume, in ft3/lb-mol
T = the gas absolute temperature, in degrees Rankine (°R)
R = the universal gas law constant of 10.7316 ft3·psia·lb-mol-l·°R-1

Gas volume is directly proportional to temperature and inversely proportional to pressure.

Below are different examples of calculation of molar volume of any ideal gas in several standard temperature and pressure reference conditions:

In SI metric units:

Vm = 8.314472 x 273.15 / 101.325 = 22.414 m3/kmol at 0 °C and 101.325 kPa absolute pressure
Vm = 8.314472 x 273.15 / 100.000 = 22.711 m3/kmol at 0 °C and 100 kPa absolute pressure

In customary USA units:

Vm = 10.7316 x 491.68 / 14.696 = 359.0441 ft3/lb-mol at 32 °F and 14.696 psia
Vm = 10.7316 x 491.68 / 14.730 = 358.2154 ft3/lb-mol at 32 °F and 14.73 psia

The only reason is to make flow rates under widely differing conditions comparable.

Converting to standard temperature and pressure or normal conditions is just a way of converting volumetric quantities into mass (or molar) based quantities.

Just think of STP or NTP as being another way of expressing mass.

There is no universally accepted Standard Temperature and Pressure or Normal Temperature and Pressure for gases.

5. Standards

There are at least a dozen or more different sets of reference temperature and pressure that are referred to as standard or normal.

The compressibility of gases means that a cubic meter of gas has different mass whenever pressure and temperature conditions change:

A m3 of air at 100 bar (a) and 40 0C has a mass of 112 kg. If the pressure and temperature conditions change, the weight of the air contained in a m3 also changes.
A m3 of air at 1.013 bar (a) (equivalent to 1 ata) and 0 0C has a mass of 1.3 kg.
One kg of air has a mass of 1 kg.

Therefore, if we express a gas flow in kg / h, the mass of gas to which we refer per unit of time is clearly defined. However, if we use a unit of volume per unit of time (as m3 / h), this information is insufficient to determine the mass of gas per unit of time, and it is essential to clarify the conditions to which the volume is determined.

In this sense, there are two options:

Express the volume of gas per unit of time under the actual flow conditions. The difficulty of this measurement is the difficult comparison of flows, even in the same application, since in front of a variation of pressure and / or temperature the flow would vary.
Express the volume of gas per unit of time under reference conditions: in this case, we express the volume at arbitrarily set pressure and temperature and used as a reference. This pressure and temperature bear no relation to those of flow. A typical reference condition is 1 absolute atmosphere and 00C, and is known as a normal condition, expressing the flow in normal cubic meters hour (Nm3 / h).

Entity	Temp (°C)	Temp (°F)	Temp (°K)	Pressure (kPa)	Pressure (psi)	Molar Vol [m3]	Molar Vol [dm3]
Standard Temperature and Pressure. IUPAC (STP) since 1982	0	32	273	100.000	145.038	0,02270	22,699
NIST, ISO 10780, formerly IUPAC (STP) until 1982	0	32	273	101.325	146.959	0,02240	22,402
Normal Temperature and Pressure. This is also called NTP.	20	68	293	101.325	146.959	0,02404	24,043
IUPAC (SATP)	25	77	298	100.000	145.038	0,02478	24,777
EPA	25	77	298	101.325	146.959	0,02445	24,453
American Association of Physicists in Medicine.	22	72	295	101.325	146.959	0,02421	24,207
AMCA, air density = 0.075 lbm/ft3. This AMCA standard applies only to air.; Compressed Gas Association [CGA] applies to industrial gas use in USA.	21	70	294	101300	14.70	0,02413	24,131
CAGI	20	68	293	100.000	145.038	0,02436	24,361
ISO 5011	20	68	293	101300	14.69	0,02405	24,049
GOST 2939-63	20	68	293	101330	14.696	0,02404	24,042
SPE, U.S. OSHA, SCAQMD	16	60	289	101330	14.696	0,02371	23,714
EGIA, OPEC, U.S. EIA; U.S. DOT	16	60	289	101600	14.73	0,02365	23,650
ICAOs ISA, ISO 13443, EEA, EGIA	15	59	288	101.325	146.959	0,02363	23,633
SPE	15	59	288	100.000	145.038	0,02395	23,946
U.S. Army Standard Metro	15	59	288	99990	14.503	0,02395	23,948
ISO 2314, ISO 3977-2	15	59	288	101330	14.696	0,02363	23,631
Federal Aviation Administration (FAA)	15	59	288	101330	14.70	0,02363	23,631

The full names of the entities are listed below :

IUPAC: International Union of Pure and Applied Chemistry
NIST: National Institute of Standards and Technology
CODATA: Committee on Data for Science and Technology
ISA: ICAOs International Standard Atmosphere
ISO: International Organization for Standardization
EEA: European Environment Agency
EGIA: Canadian Electricity and Gas Inspection Act
U.S. EPA: United States Environmental Protection Agency
SATP: Standard Ambient Temperature and Pressure
EPA: Environmental Protection Agency
AMCA: Air Movement and Control Association
CAGI: Compressed Air and Gas Institute
GOST: Gosudarstvennyy Standart
SPE: Society of Petroleum Engineers
OSHA: Occupational Safety and Health Administration
SCAQMD: South Coast Air Quality Management District
EGIA: Electricity and Gas Inspection Act
OPEC: Organization of the Petroleum Exporting Countries
EIA: Energy Information Administration
DOT: Department of Transportation
ICAO: International Civil Aviation Organization
FAA: Federal Aviation Administration

6. Conclusion

Understanding the difference between actual, standard, and normal flows is crucial for accurate measurement and comparison of gas volumes in various industrial applications. Standardized flows provide a consistent reference for calculations, making it easier to compare and interpret data across different conditions. By using standardized volumes, industries can ensure precise measurements and optimize their processes effectively.

Download our free PDF file about this article!

Rating: 4.5655 - 534 reviews

We have prepared this complete PDF so that you have all the information we give in this article and you can share it, discuss it with your colleagues, and use it professionally. Having the content in PDF format allows you to access it offline, print it easily, and keep it well-organized for future reference.

We consider that it is better to have a well-formatted text that includes all the key concepts explained in this publication, ready to share or save for later use. A PDF ensures that the layout remains intact across different devices and makes it easier to annotate or highlight important points.

Information and Definitions

Actual Flow
Actual flow refers to the flow rate of a fluid measured under real operating conditions, accounting for variations in pressure, temperature, and fluid density. Unlike standard or normal flow, actual flow reflects the true behavior of the system at a specific time, considering factors such as changes in environmental conditions or process fluctuations. It is often measured in real-time and is crucial for process control and optimization. Calculations based on actual flow provide insights into system performance but may require further adjustments to compare with other flow types like standard or normal.

Density Correction
Density correction is the process of adjusting the flow measurement to account for variations in fluid density, which may change due to temperature, pressure, or composition. In cases of actual flow, density correction ensures that flow measurements are accurately reported by compensating for these variations. When fluids are measured under actual conditions, density can fluctuate, impacting the calculated volume flow rate. The density correction factor is used to standardize or normalize the readings, allowing for more reliable comparisons with other flow measurements such as standard or normal flows.

Normal Flow
Normal flow is the flow rate of a fluid at a specified set of reference conditions, typically 0°C (273.15K) and 1 atmosphere of pressure. This standardized condition allows for consistent comparison of flow measurements across different systems and conditions. Normal flow is used primarily when comparing flow rates of gases or fluids in different environments to standardize measurements. The primary difference between normal and actual flow is that normal flow assumes ideal conditions, while actual flow represents real-world operating scenarios where temperature and pressure may vary.

Orifice Flow Calculation
Orifice flow calculation is the process of determining the flow rate through an orifice plate, often using the differential pressure created across the plate. The calculation can apply to actual, standard, or normal flows, depending on the conditions at which the measurement is taken. In actual flow, the differential pressure is corrected for the temperature and pressure of the process fluid. For standard or normal flows, additional corrections, such as temperature and pressure compensation, are applied to standardize the measurement to a reference set of conditions, allowing for accurate comparisons.

Pressure Correction
Pressure correction refers to adjusting flow measurements to account for variations in system pressure. In the case of actual flow, the pressure may fluctuate based on the operating conditions, which affects the density and compressibility of gases or liquids. Correcting for these variations ensures that the flow measurement is accurate under real conditions. When comparing with standard or normal flow rates, pressure correction is necessary to align measurements with the reference conditions of 1 atm for normal flow or the specified reference pressure for standard flow, providing a consistent basis for comparison.

Standard Flow
Standard flow is the flow rate of a fluid measured at specified reference conditions of 15°C (288.15K) and 1 atmosphere of pressure. Standard flow is commonly used in the natural gas industry and other industries to provide a consistent basis for flow measurement, independent of the operating conditions. Unlike actual flow, which is influenced by varying pressure and temperature, standard flow applies correction factors to adjust the measured flow to the standard conditions, making it easier to compare measurements across different systems or locations.

Temperature Correction
Temperature correction adjusts the flow measurement to account for temperature variations that can affect fluid properties like density and viscosity. In actual flow, the temperature of the fluid is typically measured and used to correct the flow rate. The temperature correction factor is essential because changes in temperature can significantly alter the flow characteristics, especially for gases. When comparing actual flow to standard or normal flow, temperature corrections allow for accurate adjustments, enabling the flow measurement to be standardized to the specific reference conditions, ensuring consistent and meaningful data.

Total Flow
Total flow refers to the cumulative volume or mass of fluid that has passed through a system over a given period, often used to assess overall system performance. It is typically calculated by integrating the instantaneous flow rate over time. In contrast to actual, standard, or normal flow rates, total flow accumulates the measured flow over an extended duration. The total flow measurement is helpful for tracking long-term trends in production or consumption, though adjustments for pressure, temperature, and density may be necessary when comparing total flow to other types of flow measurements.

Volumetric Flow
Volumetric flow is a measure of the volume of fluid passing through a system per unit of time, commonly expressed in cubic meters per second (m³/s) or liters per minute (L/min). This measurement can be reported as actual, standard, or normal flow depending on the reference conditions used for measurement. For actual flow, the fluid’s density and the system’s operating pressure and temperature are considered, whereas standard and normal flows apply correction factors to adjust the volume to specified conditions, such as 1 atm and 15°C, providing consistent comparisons between different systems or processes.

Flow Measurement Conversion
Flow measurement conversion is the process of converting flow measurements from actual flow conditions to standard or normal flow conditions by applying correction factors for temperature, pressure, and density. This is essential when comparing flow rates from different systems that operate under varying conditions. For example, to convert actual flow to standard flow, the flow rate must be adjusted to account for the differences in pressure and temperature between the operating conditions and the standard reference conditions. These conversions ensure that flow measurements are comparable and consistent across various applications.

Another calculators or articles that may interest you ...

1 P&ID Diagram Basics 2 - International Standards - Standard symbols in process diagrams.

2 P&ID Diagram Basics 3 - Functional Identification - Functional numbering and identification.

3 Introduction to Hazop Analysis - Hazard and operability study methodology.

4 Pressure Units Conversion - Convert between pressure measurement units.

5 Molecular Weight of Common Gases - Gas property reference data.

6 Orifice Plate Calculator - Size - Calculate orifice dimensions.

7 Flow Rate Calculator - Calculate volumetric and mass flow rates.

8 Restriction Orifice Calculator - Flow - Calculate flow through restriction orifices.

Frequently Asked Questions

Q1 What is the difference between actual, standard, and normal flows?

A1 Actual flow refers to the volume of gas or fluid flowing through a system under the specific conditions (pressure, temperature) at that moment. Standard flow is the volume measured at a reference temperature and pressure, typically 0 degrees Celsius and 1 atmosphere. Normal flow, on the other hand, is a common reference used in the industry for flow measurements, where normal conditions are defined as 20 degrees Celsius and 1 atmosphere of pressure. These definitions help standardize flow measurements across different operating conditions.

Q2 Why is it important to distinguish between actual, standard, and normal flows?

A2 Distinguishing between actual, standard, and normal flows is crucial because flow measurement varies with temperature and pressure. By using standardized conditions, engineers can compare flow rates accurately across different systems, designs, and environments. It also ensures consistent reporting and helps avoid errors when calculating energy consumption, system capacities, and equipment performance under varying conditions. Without this distinction, comparing data from different systems would be difficult and inaccurate, leading to potential design inefficiencies or operational mistakes.

Q3 How do pressure and temperature affect actual flow rates?

A3 Pressure and temperature directly influence the density of the gas or fluid, which in turn affects the flow rate. At higher temperatures, gases expand and their density decreases, resulting in a lower mass flow rate for a given volumetric flow rate. Similarly, higher pressure compresses gases, increasing their density, which can lead to a higher mass flow rate for the same volumetric flow. Therefore, actual flow rates must be adjusted for changes in temperature and pressure to ensure consistent measurement, especially when comparing systems under different operating conditions.

Q4 How do engineers convert actual flow to standard or normal flow?

A4 Engineers convert actual flow to standard or normal flow using correction factors based on temperature and pressure. For standard flow, they apply a formula that adjusts the flow based on the reference standard conditions, typically 0 degrees Celsius and 1 atmosphere of pressure. For normal flow, adjustments are made for a reference temperature of 20 degrees Celsius and 1 atmosphere. These conversions help normalize data so that it can be compared across systems with different operational environments.

Q5 How do normal conditions affect the flow measurement?

A5 Normal conditions, typically defined as 20 degrees Celsius and 1 atmosphere of pressure, are used as a baseline for flow measurement. By converting flow data to normal conditions, engineers can make consistent comparisons of systems across different environmental conditions. This standardization eliminates variations caused by changes in ambient temperature or pressure, allowing more accurate analysis of equipment performance and capacity. However, this conversion assumes that the system operates within typical ranges, and deviations from these conditions may affect the accuracy of the conversion.

Q6 Is it necessary to convert between different flow measurements in all applications?

A6 It is not always necessary to convert between different flow measurements in all applications. However, for accurate system design, maintenance, and troubleshooting, especially in large-scale industrial applications, it is essential. Conversions between actual, standard, and normal flows are critical when comparing data from various systems or ensuring consistent performance across different operating environments. In some cases, if the flow conditions are stable and closely match standard conditions, conversions may be less critical, but for safety and precision, engineers often prefer using the conversions.

Q7 What are the most common units used for measuring flow rates?

A7 The most common units used for measuring flow rates are cubic meters per hour (m³/h), cubic feet per minute (CFM), and liters per minute (LPM) for volumetric flow. For mass flow, kilograms per second (kg/s) and pounds per hour (lb/h) are frequently used. The choice of units depends on the specific application, the type of fluid or gas being measured, and the industry standard practices. Flow rate units must be consistent with the temperature and pressure conditions to ensure accurate comparisons.

Q8 What role do flow meters play in measuring actual flow?

A8 Flow meters are crucial devices for measuring actual flow in a system. They monitor the volume or mass of fluid or gas passing through a pipe or duct at any given time, providing real-time data. These instruments are essential for maintaining efficient operation, monitoring system performance, and ensuring that flow rates meet design specifications. Different types of flow meters, including electromagnetic, turbine, and thermal mass flow meters, are used depending on the fluid or gas type, flow rate range, and required accuracy.

Q9 What is a typical use case for standard flow measurement?

A9 A typical use case for standard flow measurement is in the calibration of equipment, where conditions such as pressure and temperature are controlled and set to predefined standards. Standard flow measurements are also used in regulatory and compliance testing, where consistency across different systems and facilities is necessary. For example, in the natural gas industry, standard flow measurements are used to determine energy content and bill customers, ensuring uniformity in calculations regardless of environmental variations at different locations.

Q10 Why is there a difference between actual and standard flow rates?

A10 The difference between actual and standard flow rates arises because the two are measured under different conditions. Actual flow reflects real-time conditions, including fluctuations in pressure and temperature, while standard flow is adjusted to a fixed reference temperature and pressure. As the properties of gases and fluids change with environmental conditions, such as temperature and pressure, the volumetric flow rate can vary. Standard flow measurements provide a consistent basis for comparison and analysis, whereas actual flow is more variable and dependent on specific operational conditions.