What is the difference between Actual, Standard and Normal Flows?
What are Normal Conditions of Temperature and Pressure?
This article brings you detailed information regarding normal conditions of temperature and pressure and try to solve questions like:
How to convert actual flow to normal flow?
How to convert standard cubic meter to normal cubic meter?
How actual to normal flow conversion works?
If you need to do any calculation regarding this topic feel free to use our Flow Rate Calculator:
- Rating: 4.5 - 468 reviews
You can share this article through:
Download your free PDF file about Normal and Standard Temperature and Pressure!
We have prepared this complete pdf so that you have all the information we give in this article and you can share it, discuss it with your colleagues and use it professionally.
We consider that it is better to have a well-formatted text that includes all the key concepts explained in this publication ready to share or save for later use.
1. Overview
Gas density changes with pressure and temperature, so the use of standardized volumes when referring to quantities of gas is mandatory.
Standardized volumes are commonly used in different types of industries which uses gas as raw material. The volume of gas at actual pressure and temperature must be converted to standardized volumes.
The two common standardized volumes are standard cubic feet (scf) and normal cubic meters (Nm3).
A standard cubic foot of gas corresponds to 1 cubic foot of gas at 32 °F (0 °C) and 14.6959 PSI, and a normal cubic meter of gas corresponds to 1 cubic meter at 20°C at 101.325 kPa (NIST Reference). We will see later that it is important to list the temperature and pressure being used as standard, since many standards are used worldwide.
Why we use the standardized flows instead of simple volumetric flow?
We use standardized flows to make calculations easy.
For example, if we are compressing 125 Nm3/min air from 1 bar to 25 bar pressure then the volumetric flow through the compressor will remains same in Nm3/min but this is not the case for the volumetric flow in actual conditions.
The gas being compressible, it is possible to change a volume of the same amount of gas by compressing or changing its temperature.
It becomes very difficult to define a quantity of gas volume without relating this value with the pressure and temperature when the volume was measured.
Usually is not easy to define the temperature and pressure of a volume of gas, this is why normally we use standardized volumes referred to a define set of temperature and pressure measurements. We call this conditions normalized or standard.
1.1. STP vs NTP
- STP means Standard Temperature and Pressure.
- NTP means Normal Temperature and Pressure.
1.2. Normal Cubic Meter (nm3/h) vs Actual Cubic Meter (am3/h)
- Nm3/h refers to flow of gas at normal temperature and pressures.
- Am3/h refers to flow of gas at current operating conditions of the process.
2. What are the standard temperature and pressure applications?
Standard or normal conditions are used as reference values in thermodynamics of gases. To specify the gas volume, Normal or Standard temperature and pressure conditions are generally used.
The reason is very simple, the volume of a constant number of moles of gas depends on the measurements of temperature and pressure.
Due to this reason, whenever the quantity of gas is specified in terms of gas volume, it is necessary to define the corresponding temperature and pressure conditions for the volume measurement.
Therefore, we can use the reference temperature and pressure conditions to specify the volume of gas measured under those conditions. Once the volume is calculated, we can convert the calculated amount into an amount of moles or mass of gas.
There are different standards that define different temperature and pressure values. These standards depend on the organization that defines them. In general, the standard pressure is close to atmospheric pressure and the standard temperature is close to the ambient temperature value.
3. Gas properties
The gases by definition are in a gaseous state, under defined pressure and temperature (for example, the nitrogen we breathe). Steam and vapors are liquids in the conditions described above, although thermodynamically there is no difference between vapor / vapors and gases.
A fundamental difference between liquids and gases is their compressibility (liquids are generally considered incompressible). The compressibility is a property of the matter to which it causes that all the bodies diminish of volume when subjecting them to a pressure or compression determined keeping other parameters constant.
Another important property of gases is that their volume will increase with the increase in temperature, a property of the gas used in hot air balloons.

The description of the relationship of these properties is given by the Law of Ideal Gas:

where (in SI metric units):
- P = the gas absolute pressure, in Pa
- n = number of moles, in mol
- V = the gas molar volume, in m3/mol
- T = the gas absolute temperature, in K
- R = the universal gas law constant of 8.314472 m3·Pa·mol-1·K-1
or where (in customary USA units):
- P = the gas absolute pressure, in psia
- n = number of moles, in lb-mol
- V = the gas molar volume, in ft3/lb-mol
- T = the gas absolute temperature, in degrees Rankine (°R)
- R = the universal gas law constant of 10.7316 ft3·psia·lb-mol-l·°R-1
The mass of a gas will remain constant but the volume and density will change with pressure and temperature (law of conservation of mass).
If you need to do any calculation regarding this topic feel free to use our Flow Rate Calculator:
For this reason, we will use mass instead of volume as a much more relevant term for measuring.
Usually, gases like compressed air or natural gas are measured using standardized molar volume (eg Scf or Nm3).
These terms at the first glance look like volumetric terms, which they are not. Corrected Volume is defined as mass over the density at reference conditions (eg at 0°C and 1013.25mbar; 1.29kg/m3 for air), thus it is a mass term.
A volumetric flow rate with units of CFM or m3 implies that the flow rate was measured at actual conditions (actual pressure, actual temperature).
The distinction between Standardized and Actual is important because it implies that his density changes with pressure and temperature.
This can be seen from taking a look at the ideal gas law. As you may remember, density = mass/volume.
When the ideal gas law is rearranged, the gas density can be seen to be proportional to pressure, and inversely proportional to temperature.
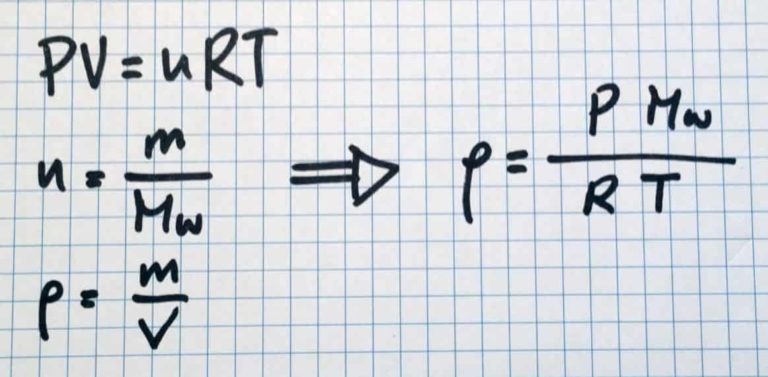
If we take Air for example, Air density at standard conditions is .0752 lb/ft3.
Since the air density of an air flow stated at standard conditions (SCFM) is always the same, it is essentially a mass flow rate!
Stating an air flow in units of SCFM makes it easy to compare conditions, and certain calculations simpler.
ρ = m/V → m = ρV →m/t = ρ (V/t)
mass flow rate = density* Volumetric flow rate.
In systems with vacuum pumps, blowers, compressors, and heat exchangers, air pressure and temperature are constantly changing, which means the actual volume flow is changing. This makes the specification of volume flow particularly prone to error and misinterpretation. Unless there is a leak, the mass / standard volume flow stays the same, so it is more concise to discuss these systems in terms of mass or standard volume flow. Specify mass or standard volume ...be understood!
Usually, Normal Volume is considered as a unit of mass for gases equal to the mass of the reference volume measured at a pressure and temperature of reference conditions.
For example, Ndm3 is a unit of mass for gases equal to the mass of 1 liter (0.035 3147 ft3) at a pressure of 1 atmosphere and at a standard temperature, often 0 °C (32 °F) or 20 °C (68 °F).
To convert from Normal or Standard Conditions to Actual (Operating) Conditions the molar gas volume is needed.
The molar gas volumes can be calculated with an accuracy that is usually sufficient by using the ideal gas law:

where (in SI metric units):
- P = the gas absolute pressure, in Pa
- n = number of moles, in mol
- V = the gas molar volume, in m3/mol
- T = the gas absolute temperature, in K
- R = the universal gas law constant of 8.314472 m3·Pa·mol-1·K-1
or where (in customary USA units):
- P = the gas absolute pressure, in psia
- n = number of moles, in lb-mol
- V = the gas molar volume, in ft3/lb-mol
- T = the gas absolute temperature, in degrees Rankine (°R)
- R = the universal gas law constant of 10.7316 ft3·psia·lb-mol-l·°R-1
Gas volume is directly proportional to temperature and inversely proportional to pressure.
Below are different examples of calculation of molar volume of any ideal gas in several standard temperature and pressure reference conditions:
- In SI metric units:
- Vm = 8.314472 x 273.15 / 101.325 = 22.414 m3/kmol at 0 °C and 101.325 kPa absolute pressure
- Vm = 8.314472 x 273.15 / 100.000 = 22.711 m3/kmol at 0 °C and 100 kPa absolute pressure
- In customary USA units:
- Vm = 10.7316 x 491.68 / 14.696 = 359.0441 ft3/lb-mol at 32 °F and 14.696 psia
- Vm = 10.7316 x 491.68 / 14.730 = 358.2154 ft3/lb-mol at 32 °F and 14.73 psia
The only reason is to make flow rates under widely differing conditions comparable.
Converting to standard temperature and pressure or normal conditions is just a way of converting volumetric quantities into mass (or molar) based quantities.
Just think of STP or NTP as being another way of expressing mass.
There is no universally accepted Standard Temperature and Pressure or Normal Temperature and Pressure for gases.
4. Standards
There are at least a dozen or more different sets of reference temperature and pressure that are referred to as standard or normal.
The compressibility of gases means that a cubic meter of gas has different mass whenever pressure and temperature conditions change:
- A m3 of air at 100 bar (a) and 40 0C has a mass of 112 kg. If the pressure and temperature conditions change, the weight of the air contained in a m3 also changes.
- A m3 of air at 1.013 bar (a) (equivalent to 1 ata) and 0 0C has a mass of 1.3 kg.
- One kg of air has a mass of 1 kg.
Therefore, if we express a gas flow in kg / h, the mass of gas to which we refer per unit of time is clearly defined. However, if we use a unit of volume per unit of time (as m3 / h), this information is insufficient to determine the mass of gas per unit of time, and it is essential to clarify the conditions to which the volume is determined.
In this sense, there are two options:
- Express the volume of gas per unit of time under the actual flow conditions. The difficulty of this measurement is the difficult comparison of flows, even in the same application, since in front of a variation of pressure and / or temperature the flow would vary.
- Express the volume of gas per unit of time under reference conditions: in this case, we express the volume at arbitrarily set pressure and temperature and used as a reference. This pressure and temperature bear no relation to those of flow. A typical reference condition is 1 absolute atmosphere and 00C, and is known as a normal condition, expressing the flow in normal cubic meters hour (Nm3 / h).
| Entity | Temp (°C) | Temp (°F) | Temp (°K) | Pressure (kPa) | Pressure (psi) | Molar Vol [m3] | Molar Vol [dm3] |
|---|---|---|---|---|---|---|---|
| Standard Temperature and Pressure. IUPAC (STP) since 1982 | 0 | 32 | 273 | 100.000 | 145.038 | 0,02270 | 22,699 |
| NIST, ISO 10780, formerly IUPAC (STP) until 1982 | 0 | 32 | 273 | 101.325 | 146.959 | 0,02240 | 22,402 |
| Normal Temperature and Pressure. This is also called NTP. | 20 | 68 | 293 | 101.325 | 146.959 | 0,02404 | 24,043 |
| IUPAC (SATP) | 25 | 77 | 298 | 100.000 | 145.038 | 0,02478 | 24,777 |
| EPA | 25 | 77 | 298 | 101.325 | 146.959 | 0,02445 | 24,453 |
| American Association of Physicists in Medicine. | 22 | 72 | 295 | 101.325 | 146.959 | 0,02421 | 24,207 |
| AMCA, air density = 0.075 lbm/ft3. This AMCA standard applies only to air.; Compressed Gas Association [CGA] applies to industrial gas use in USA. |
21 | 70 | 294 | 101300 | 14.70 | 0,02413 | 24,131 |
| CAGI | 20 | 68 | 293 | 100.000 | 145.038 | 0,02436 | 24,361 |
| ISO 5011 | 20 | 68 | 293 | 101300 | 14.69 | 0,02405 | 24,049 |
| GOST 2939-63 | 20 | 68 | 293 | 101330 | 14.696 | 0,02404 | 24,042 |
| SPE, U.S. OSHA, SCAQMD | 16 | 60 | 289 | 101330 | 14.696 | 0,02371 | 23,714 |
| EGIA, OPEC, U.S. EIA; U.S. DOT | 16 | 60 | 289 | 101600 | 14.73 | 0,02365 | 23,650 |
| ICAOs ISA, ISO 13443, EEA, EGIA | 15 | 59 | 288 | 101.325 | 146.959 | 0,02363 | 23,633 |
| SPE | 15 | 59 | 288 | 100.000 | 145.038 | 0,02395 | 23,946 |
| U.S. Army Standard Metro | 15 | 59 | 288 | 99990 | 14.503 | 0,02395 | 23,948 |
| ISO 2314, ISO 3977-2 | 15 | 59 | 288 | 101330 | 14.696 | 0,02363 | 23,631 |
| Federal Aviation Administration (FAA) | 15 | 59 | 288 | 101330 | 14.70 | 0,02363 | 23,631 |
The full names of the entities are listed below :
- IUPAC: International Union of Pure and Applied Chemistry
- NIST: National Institute of Standards and Technology
- CODATA: Committee on Data for Science and Technology
- ISA: ICAOs International Standard Atmosphere
- ISO: International Organization for Standardization
- EEA: European Environment Agency
- EGIA: Canadian Electricity and Gas Inspection Act
- U.S. EPA: United States Environmental Protection Agency
- SATP: Standard Ambient Pressure and Temperature
- CAGI: Compressed Air and Gas Institute
- SPE: Society of Petroleum Engineers
- OSHA: U.S. Occupational Safety and Health Administration
- SCAQMD: Californias South Coast Air Quality Management District
- OPEC: Organization of Petroleum Exporting Countries
- EIA: U.S. Energy Information Administration of the U.S. Department of Energy
- Std. Metro: U.S. Armys Standard Metro (used in ballistics)
- AMCA: Air Movement and Control Association (the AMCA standard applies only to air)
5. References
Another articles that may interest you:
- Orifice Plate Installation Guidelines is a necessary set of rules if you need to install an Orifice Plate
- What is pressure compensation? and why temperature compensation is required? In this article are all answers
- In the Instrument Simulation Laboratory you have a tool to see the relationship between a tank level measurement located in the field and its visualization in the control room.
- A complete list of the indispensable books that every professional in process control engineering must have, with prices and direct links to buy them if you want.
- In Flow Rate Calculator you can calculate the volumetric flow rate of any liquid or gas through a specific pipe diameter and download results.
- Volumetric Flow Converter, another of our useful free online calculators .
- If you need a Restriction Orifice Calculator, these are your tools.
Any question?
If you have any question regarding this article, please don't hesitate to get in touch ... Anyway you can have a look at our frequently asked questions page, there you will find a solution to the most common questions.